por Iván José Turmero Astros

Continuación de este post.
.
Para elaborar pronósticos se pueden encontrar dos grandes clases de modelos: causales y de series de tiempo. Los primeros tratan de encontrar las relaciones de causalidad entre diferentes variables, de manera que conociendo o prediciendo alguna o algunas de ellas, se pueda encontrar el valor de otra. En el segundo caso no interesa encontrar esas relaciones, sino que se requiere solamente encontrar los posibles valores que asumirá una determinada variable. En todos los casos siempre se hace uso de la información histórica, ya sea para predecir el comportamiento futuro o para suponer que el comportamiento histórico se mantendrá hacia el futuro y sobre esta base hacer los estimativos.
Se debe tener presente que no existe ningún método de pronóstico infalible; lo que hacen estos procedimientos es estimar un valor posible, pero siempre sujeto a errores. Si el fenómeno que se va a pronosticar fuera determinístico, sólo bastaría utilizar la ley matemática que lo rige y predecir con exactitud el resultado; este sería el caso de fenómenos físicos, como por ejemplo la caída libre de un cuerpo. En el proceso de toma de decisiones se involucra el comportamiento humano, por ejemplo, a través de las decisiones de los individuos a quienes está dirigida un determinado producto o servicio; las decisiones del mercado están compuestas por muchísimas decisiones individuales, imposibles de predecir con exactitud.
La mayoría de los datos incluyen combinaciones de estas tendencias y se deben generar procedimientos para separarlos. Existen otras clases de pronósticos denominados cualitativos o de pronóstico tecnológico, tales como el Método Delphi.
Este método busca, a través de múltiples rondas o iteraciones donde se comparte la información, encontrar consenso sobre valores o escenarios posibles. Se hace énfasis en que no hay un método de pronóstico perfecto, aunque se podría construir un modelo que ajuste perfectamente los datos que se tienen de un fenómeno; sin embargo, esto no es recomendable puesto que el elemento aleatorio o de error siempre estará presente y será impredecible y es mejor identificar los patrones predecibles y asumir el error que se presente que tratar de introducir en el modelo el elemento error que, se repite, es completamente impredecible e inevitable. En otras palabras, cualquier estimativo implica un cierto grado de error inevitable.
- Métodos de los mínimos cuadrados
Se considera el mejor método aquel que minimiza la suma de los cuadrados de los errores (diferencias entre el valor estimado y el observado).
Dentro de los métodos de suavización se pueden considerar tres categorías: a) Promedios móviles, b) suavización exponencial y c) otros.
Promedios móviles
Esta técnica consiste en tomar un grupo de valores observados, calcularle el promedio y utilizarlo como pronóstico para el siguiente período. Sólo sirve para pronosticar un sólo período: el siguiente. Se debe especificar el número de observaciones que se tomarán; se llama móvil porque siempre se toman las N últimas observaciones para hacer el pronóstico. Se pueden considerar promedios móviles simples y promedios móviles lineales. En el primer caso se toman los N últimos datos y se calcula el promedio; en el segundo caso se construyen además promedios de los promedios y con ellos se establece una ecuación lineal que permite elaborar el pronóstico.
Este método puede utilizarse cuando se sabe que los datos son estacionarios. La ventaja sobre el promedio total es que permite ajustar el valor de N para que responda al comportamiento de los datos.
Suavización exponencial:
Existen muchos métodos de suavización exponencial: simple, de tasa de respuesta de adaptación, método de Brown de un solo parámetro, método de Holt de dos parámetros, método cuadrático de Brown, etc. Aquí se considerarán un método de suavización: suavización exponencial simple.
El suavización exponencial simple consiste en asignar un peso a la última información (dato) disponible y al último pronóstico, el cual, a su vez, contiene la información pasada, así:
F t+1 = aX t + (1- a) F t
Para F 2, se tiene:
F 2 = F 1
Otra forma de expresar el pronóstico es:
F t+1 = F t + a e
Donde e es el error incurrido en el último pronóstico.
Uno de los métodos más conocidos, pero también de los más mal utilizados es la regresión lineal. En cualquier curso de Presupuesto es tema obligado. Sin embargo, como se mencionó, se tiende a utilizar mal este procedimiento. En cualquier caso en que se utilice un modelo, es necesario validarlo: esto es, verificar si los supuestos del modelo coinciden con la realidad. Y esto no es lo que hace la mayoría de los usuarios.
La regresión lineal implica por lo menos, distribución normal de los errores de la variable dependiente, que no están correlacionados y para utilizarlo con validez estadística, además debe contarse con un tamaño de muestra n de por lo menos 30 datos históricos. Un supuesto obvio es que la tendencia observada de los datos puede ser descrita por una recta. Sin embargo, este supuesto se puede obviar haciendo las substituciones necesarias, por ejemplo, si se considera que una variable tiene un comportamiento exponencial (no lineal), estos datos podrían “linealizarse” calculando el logaritmo de los datos y proyectar el logaritmo. Después se halla el antilogaritmo y esa sería la proyección.
La idea de la regresión lineal es hallar una recta que cumpla con un requisito básico común para muchos métodos de pronóstico: la suma de los cuadrados de la diferencia entre el valor estimado y el observado es mínima. Por eso se llama también método de mínimos cuadrados. En general, se trata de encontrar (en el caso de la regresión lineal), una recta que cumpla esa condición y que se expresa así:
Y = a + b1X1 + b2X2 + b3X3+…+bnXn + e
Donde
Y = variable dependiente
Xj = variable independiente
e = error
a = intersección con el eje de las abscisas (y)
bj = coeficiente de cada variable Xj
El caso particular de una variable independiente la “fórmula” será:
Y = a + bX + e
- Métodos de descomposición
Un método de pronóstico es el de descomposición, para analizar series de tiempo. Un paso importante en el proceso de determinar el método de series de tiempo adecuado es considerar los diferentes patrones que se encuentran en los datos. Se pueden identificar cuatro patrones típicos: horizontal o estacionaria, estacional, cíclico y de tendencia.
- Se presenta un patrón horizontal o estacionario (H) cuando los datos fluctúan alrededor de un valor promedio constante. Las ventas que no aumentan ni disminuyen con el tiempo, es un ejemplo de este tipo de comportamiento.
- Se presenta un patrón estacional (E) cuando los datos están afectados por factores que se repiten con cierta frecuencia (trimestral, mensual o en determinadas fechas, por ejemplo, Navidad, Semana Santa, etc.).
- Un patrón cíclico (C) se presenta debido a efectos económicos de largo plazo y generalmente asociados con el ciclo económico. La construcción de vivienda puede ser un ejemplo de este tipo.
- Un patrón cíclico (C) se presenta debido a efectos económicos de largo plazo y generalmente asociados con el ciclo económico. La construcción de vivienda puede ser un ejemplo de este tipo.
Los métodos de descomposición suponen que los datos contienen patrones estacionales, cíclicos y de tendencia; una función que representa esta relación puede ser la siguiente:
Dato = patrón + error = f (tendencia, estacionalidad, ciclo) + error
X t = f(T t , E t , C t , Er t )
Donde:
X t es el dato al período t.
T t es el componente de tendencia en el período t.
E t es el componente o índice de estacionalidad del período t.
C t es el componente cíclico del período t.
Y Er t es el error del período t.
El procedimiento general para aislar los diversos componentes es el siguiente y se aplica a los diferentes métodos de descomposición.
1) Con los datos disponibles calcule el promedio con un N igual a la longitud de la estacionalidad (12 meses, 6 meses, 4 trimestres, o 7 días, por ejemplo). Con esto se elimina la estacionalidad y el error, por lo tanto en el promedio móvil se encuentra sólo la tendencia y el ciclo. A esto lo llaman algunos desestacionalizar la serie de datos.
2) Separe el resultado del promedio móvil de los datos. Lo que queda es la estacionalidad y el error.
3) Aísle los factores estacionales promediándolos para cada período que constituyen el período completo de estacionalidad (cada mes, semestre o trimestre, por ejemplo).
4) Identifique la forma de la tendencia con los resultados de (lineal, exponencial, etc.) y calcule su valor para cada uno de los períodos para los cuales se tienen datos.
5) Separe el resultado de 4) de los resultados de 1) para obtener el factor cíclico.
6) Separe la estacionalidad, la tendencia y el ciclo de los datos para obtener el error.
Este método es útil cuando se considera que existe una tendencia y estacionalidad. La estacionalidad se puede identificar en los datos si se observan ciertos “picos” o “baches” en los datos con regularidad; por ejemplo, si encuentra que el consumo de gaseosa es siempre mayor en los días sábados y domingos y menor en los días jueves, se podría sospechar que existe una estacionalidad asociada a esos días de la semana. Por otro lado, se puede llegar a la conclusión acerca de la existencia de la estacionalidad deduciéndola a partir del comportamiento del negocio; por ejemplo, antes de examinar cualquier dato, se podría pensar que la venta de juguetes o de calendarios y agendas va a presentar picos en los tres últimos meses del año. Obsérvese que se habla de estacionalidad cuando los períodos de análisis son menores de un año. Por ejemplo, semestres, trimestres o meses en relación con un año; quincenas, décadas o semanas en relación con mes; días de la semana con relación a la misma. Esto es, si los datos son anuales, por ejemplo, no tiene sentido pensar en la existencia de un patrón estacional. Uno de los modelos de descomposición más utilizados es el multiplicativo, o sea,
X t = T t x E t x C t x Er t
Donde:
Xt es el dato real en período t
Tt es el valor de la tendencia en período t
Ct es el valor del factor de ciclo en período t
Ert es el error en período t
Al aplicar los seis pasos propuestos se tiene:
1) y 2) Calcule el promedio móvil y aísle los factores estacionales:
Mt = Tt x Ct
Donde Mt es el promedio móvil en período t
La expresión anterior aísla la estacionalidad y el error.
3) El siguiente paso es eliminar el error de los valores obtenidos con la última expresión. Los modelos clásicos de descomposición utilizan el enfoque del promedio medial. Para calcular el promedio medial se toman todos los datos de promedio móvil para cada período (mes, trimestre, etc.) y se eliminan los valores extremos, con los datos restantes se calcula el promedio. Los datos obtenidos para cada período se ajustan al 100% multiplicando el promedio medial por 100x número de períodos/suma de todos los promedios mediales 4) y 5) Los pasos finales es el de calcular la tendencia y separarla del ciclo. Se identifica el patrón de la tendencia y se calcula el valor de ella para cada uno de los períodos para los cuales se tienen datos. La tendencia se calcula a partir de los datos Mt. En este modelo se elimina así: donde a,b,c… son las constantes de la regresión y t es el período correspondiente.
6) Con estos factores, estacionalidad, tendencia y ciclo, se puede estimar el error.
Método de determinación a través de las probabilidades subjetivas
Es importante precisar que lo subjetivo no implica arbitrariedad. Así, por ejemplo, si hoy al salir por la mañana se observa que el cielo está cubierto, entonces se saldrá preparado para la lluvia. Subjetivamente, aunque no en forma arbitraria, se está asignando una probabilidad alta al evento lluvia. Y no es arbitrario porque es el resultado de la información con que se cuenta, la cual permite hacer un estimativo subjetivo, no arbitrario, de la probabilidad de tener un día lluvioso.
Hecho esto se debe hacer una verificación de consistencia interna con la percepción de la o las personas que están haciendo la estimación subjetiva de la distribución de probabilidad. Una aproximación podría ser verificar si los valores asignados a cierto intervalo, por ejemplo, de 0 a 34,999, debe tener o no una probabilidad igual al intervalo 35,000 a 44,999 y así para todas las posibilidades. Tratar de definir el punto del intervalo que hace indiferente a la persona entre ese valor y una unidad más o una unidad menos, tiende a ser difícil en la práctica; sin embargo, siendo menos riguroso el método, se podría intentar establecer sub-intervalos iguales y hacer las verificaciones respectivas.
Una alternativa para estimar casos concretos de probabilidades subjetivas es a partir de los datos máximo, mínimo y más probable de una determinada variable. Con esta información se pueden hacer estimativos de los parámetros de algunas distribuciones, por ejemplo:
Donde:
X min = Estimativo del mínimo valor que puede tomar la variable X
X máx. = Estimativo del máximo valor que puede tomar la variable X
X p = Estimativo del valor más probable que puede tomar la variable X
s = Desviación estándar de la variable X
Estos estimativos pueden ser adecuados para distribuciones normales o distribuciones llamadas Beta utilizadas en los análisis de redes tipo PERT(Project Evaluation Review Technique).
Las probabilidades subjetivas cumplen las mismas reglas que las probabilidades objetivas y pueden ser utilizadas operacionalmente en la misma forma que las segundas.
Método de determinación de los estimativos a través de encuestas
Se presenta un ejemplo simple de cómo determinar probabilidades a partir de la información de una encuesta que contiene información subjetiva, para hacer estimativos de demanda. Parte de una encuesta a los elementos de una muestra de 200 clientes potenciales, para un determinado producto.
La encuesta precisaba varios factores de compra: 1) Deseo de comprar el producto. 2) Tiempo en que se compraría el producto. 3) Actitud de las esposas ante la decisión de compra. 4) Preocupación de que el producto utilizará energía atómica. 5) Actitud del decisor ante el precio.
Los resultados del primer punto fueron:
Respuesta Número Porcentaje
Definitivamente comprarán 10.5
Más probable que compren a que no compren 70 35
No es probable que compren 120 60
Una encuesta realizada anteriormente indicaba que con un producto similar, solo el 46% de quienes habían afirmado que comprarían, efectivamente compraron. Esta información ayuda a estimar unos pesos o ponderaciones. Con los resultados a la mano, se procedió a asignar ponderaciones a las diferentes respuestas (en este proceso se podría utilizar el Método Delphi), así:
Para el factor 1,
Respuesta Ponderación
Definitivamente comprarán 1.0
Más probable que compren a que no compren 0.4
No es probable que compren 0.0
Para el factor 2,
Respuesta Ponderación
En 3 meses 1.0
Entre 3 y 6 meses 0.8
Entre 6 y 12 meses 0.6
Para el factor 3,
Respuesta Ponderación
La esposa no opina 1.0
La esposa opina y desea el producto 1.0
La esposa opina pero prefiere a la competencia 0.6
Para el factor 4,
Respuesta Ponderación
No le preocupa el uso de energía atómica 1.0
Muestra preocupación por el uso de energía atómica 0.4
Para el factor 5,
Respuesta Ponderación
Precio dentro del presupuesto 1.0
Precio más alto que el presupuesto 0.3
Precio más bajo que el presupuesto 0.8
De acuerdo con los resultados del primer punto, o sea la pregunta sobre si comprarán o no el producto, el mercado potencial era de 40% (355 que respondieron más probable que compren), compuesto por 35% que respondió más probable que compren, más 5% que respondió que definitivamente comprarían; considerando las ponderaciones de los diversos factores, se llega a un nuevo estimativo de 19%, teniendo en cuenta solo el primer factor. (10×1+70x.4=38 y 38/200=.19)
¿Cómo se utilizarían estos pesos o ponderaciones en la estimación total? Cada Encuestado se ponderaría por la forma en que hubiera respondido así: Si el encuestado responde “bien” a todas las preguntas equivaldría a 1(1x1x1x1x1). Si por el contrario responde así:
Factor Respuesta Ponderación
1 1 1.0
2 2 0.8
3 2 1.0
4 2 0.4
5 1 1.0
Al efectuar la “Ponderación “de esas respuestas se hallaría que equivale a 0.32. Esto se repite para cada una de las encuestas y se suma; el resultado total expresaría una cifra representativa del mercado potencial. Si por ejemplo, esta suma resultara ser de 11.9, se tendría un estimativo del mercado que realmente compraría el producto de 5.95% (11.9/200).
Algunos pueden objetar la validez de hacer estimativos que no pueden ser “probados” o “demostrados” a priori y que por lo tanto la decisión podría estar tan errada como suponer la certeza de un solo estimativo. Lo cierto es que es mucho más razonable examinar varias posibilidades planteadas por expertos, que pensar que el futuro es determinístico y basar el análisis en un solo dato.
Se dice también que quienes responden una encuesta, no saben realmente cuál va a ser su comportamiento futuro y que esto es válido en cualquier dirección (los que dicen sí y los que dicen no) y que por lo tanto, cualquier intento que se haga en ese sentido, será un esfuerzo inútil. Esto indica una actitud derrotista que llevaría a la conclusión de que no se podrían tomar decisiones a menos que existiera certeza absoluta sobre el futuro. No debe olvidarse que el problema básico del decisor, es tomar decisiones con consecuencias irreversibles, con información incompleta.
La realidad es que el mundo sigue su curso. El hombre es el motor y tiene que tomar decisiones, con o sin información, completa o incompleta, confiable o no. Y mientras tanto habrá que buscar formas que despejen la incógnita del futuro y las que se presentan en este capítulo y otras de la literaturaexistente, son aproximaciones a la solución del problema.
Cómo tomar decisiones con información probabilística:
Una vez se ha obtenido la probabilidad de que un proyecto es bueno o malo, poco se puede decir sobre el curso de acción que debe emprender el decisor, puesto que es el individuo en forma subjetiva quien decide si una probabilidad de fracaso es alta o baja. O sea que el decisor deberá discernir en forma subjetiva si un proyecto con una determinada probabilidad de fracaso de considerase aceptable o no; hecha esta escogencia para proyectos mutuamente excluyentes se debe proceder a seleccionar el mejor. ¿Qué decir entonces de un proyecto con VPN esperado de $10,000,000 con probabilidad de fracaso de 10% comparado con un proyecto de $20,000,000 de VPN esperado pero con 15% de probabilidad de fracaso? Para estos casos se puede sugerir el siguiente procedimiento heurístico (no siempre escoge el mejor): se debe seleccionar el proyecto con mayor Coeficiente de Variación Probabilístico (CVP).
Problemas
1) Una encuesta de viviendas incluyó una pregunta sobre el número de automóviles, N, actualmente poseídos por gente que vive en residencias y la tasa de interés, i, sobre el préstamo de tasa más baja para los autos. Los resultados para 100 viviendas se muestran a continuación:
|
Número de autos, N
|
0
|
1
|
2
|
3
|
(4
|
|
Viviendas
|
12
|
56
|
26
|
3
|
3
|
|
Tasa de préstamo, i
|
0.00-2
|
2.01-4
|
4.01-6
|
6.01-8
|
8.01-10
|
10.01-12
|
|
Viviendas
|
22
|
10
|
12
|
42
|
8
|
6
|
(a) Determine si cada variable es discreta o continua y diga por qué.
(b) Elabore gráficas de las distribuciones de probabilidad y de las distribuciones acumulativas para N e i.
(c) De la información obtenida, ¿cuál es la probabilidad de que una vivienda tenga 1ó 2 autos?, ¿Tres o más autos?
Solución:
a) El número de autos (N) es una variable discreta, al igual que el número de viviendas, debido a que nadie puede tener un número fraccional de carros ni viviendas. Por otra parte, la tasa de préstamo es una variable continua, ya que puede asumir valores fraccionales.
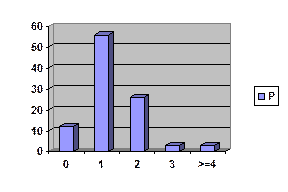
b)
|
Número de autos
|
Viviendas
|
P
|
F
|
|
0
|
12
|
12
|
12
|
|
1
|
56
|
56
|
68
|
|
2
|
26
|
26
|
94
|
|
3
|
3
|
3
|
97
|
|
(4
|
3
|
3
|
100
|
|
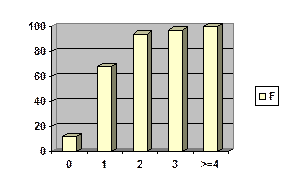
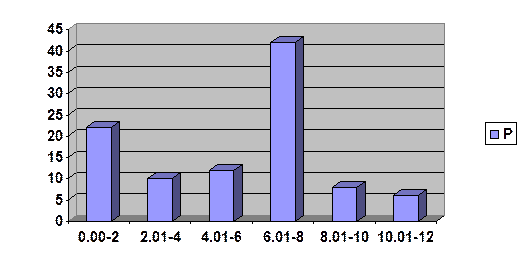
Tasa de préstamo
|
Viviendas
|
P
|
F
|
|
0.0-2
|
22
|
22
|
22
|
|
2.01-4
|
10
|
10
|
32
|
|
4.01-6
|
12
|
12
|
44
|
|
6.01-8
|
42
|
42
|
86
|
|
8.01-10
|
8
|
8
|
94
|
|
10.01-12
|
6
|
6
|
100
|
c) La probabilidad de que una vivienda tenga dos o más autos es:
P (N = 1 ó N = 2) = P (N = 1) + P (N=2) = 0,56 + 0,26 = 0,82 = 82%
La probabilidad de que una vivienda tenga tres o más autos es:
P (N ( 3) = P (N = 3) + P (N ( 4) = 0,03 + 0,03 = 0,06 = 6%
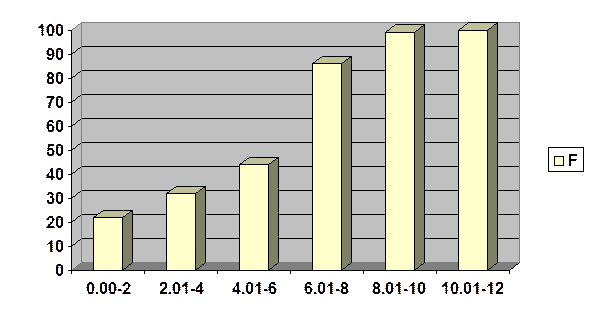
2) Un funcionario de la firma State Lottery Commission ha obtenido una muestra de los compradores de billetes de lotería durante un periodo de 1 semana en una localidad. Las cantidades distribuidas de vuelta a los compradores y las probabilidades asociadas para 5000 boletas son:
|
Distribución, $
|
0
|
2
|
5
|
10
|
100
|
|
Viviendas
|
0,91
|
0,045
|
0,025
|
0,013
|
0,007
|
(a) Elabore gráfica de la distribución acumulativa de las ganancias.
(b) Calcule el valor esperado de la distribución de los dólares por billete.
(c) Si todos los billetes cuestan $2, ¿cuál es el ingreso de largo plazo esperado para el estado por billete, con base en esta muestra?
Solución:
a)
|
Distribución
|
Probabilidad
|
Dist. Acumulada
|
|
0
|
0,91
|
0,91
|
|
2
|
0,045
|
0,955
|
|
5
|
0,025
|
0,98
|
|
10
|
0,013
|
0,993
|
|
100
|
0,007
|
1
|
b) E (D) = 0. 0,91 + 2. 0,045 + 5. 0,025 + 10. 0,013 + 100. 0,007
E (D) = 1,045 $
c) E = 2 – 1,045 = 0,955 $/billete
3) Jerry Hill es presidente y ejecutivo principal de una firma estadounidense de procesamiento de alimentos, Hill Products and Services. Recientemente, fue contactado por una gran cadena de supermercados con sede en Indonesia, que desea el mercadeo dentro del país de su propia marcade cenas congeladas, bajas en grasa, con calorías que varían dentro de un rango medio, de mucho sabor, para ser calentadas en microondas. La ofertahecha a Jerry por la corporación del supermercado exige que se tome una serie de decisiones, ahora y dentro de 2 años. La decisión actual comprende dos alternativas: (1) Arrendar las instalaciones de la cadena de supermercados, que se había acordado convertir en una instalación de procesamiento actual para uso inmediato por parte de la compañía de Jerry, o (2) construir y adquirir una instalación de procesamiento y empaque en Indonesia. Los resultados posibles de esta primera etapa de decisión son un buen o mal mercado dependiendo de la respuesta del público.
Las alternativas de decisión, 2 años a partir de ahora, dependen de la decisión de arrendar o adquirir que se tome ahora. Si Hill decide arrendar; una buena respuesta del mercado significa que las alternativas de decisión futuras son producir al doble del volumen, a igual volumen o a la mitad del volumen original. Ésta será una decisión mutua entre la cadena de supermercados y la compañía de Jerry. Una respuesta mala del mercado indicará la mitad del nivel de producción, o el retiro completo del mercado de Indonesia. Los resultados para decisiones futuras son, nuevamente, buenas y malas respuestas del mercado.
Como acordó la compañía del supermercado, la decisión actual para Jerry de adquirir la instalación le permitirá fijar el nivel de producción dentro de 2 años. Si la respuesta del mercado es buena, las alternativas de decisión son cuatro veces o el doble de los niveles originales. La reacción a una mala respuesta del mercado será la producción al mismo nivelo ninguna producción.
Construya el árbol de decisiones y resultados para Hill Products and Services.
Solución
Identifique los nodos y las ramas de decisión iniciales y luego desarrolle el árbol utilizando las ramas y los resultados de mercado bueno y malo para cada decisión. La figura 6 detalla la primera etapa de decisión (DI) y las ramas de resultados.
 Decisión ahora:
Decisión ahora:
Llámela DI
Alternativas: arrendar (L) y adquirir (O)
Resultados: buenos y malos mercados
 Selección de decisiones dentro de 2 años:
Selección de decisiones dentro de 2 años:
Llámelas D2 hasta D5
Resultados: buen mercado, mal mercado y fuera del negocio.
 Selección de niveles de producción para D2 hasta D5:
Selección de niveles de producción para D2 hasta D5:
Cuadruplique la producción (4X); duplique la producción (2X); nivel de producción (1 X); la mitad de la producción (O.5X); suspenda la producción (OX).
Las alternativas para futuros niveles de producción (D2 hasta D5) se agregan al árbol seguidas de las buenas y malas respuestas del mercado (figura 6). Si se toma la decisión de suspender la producción (OX) en D3 o D5, el único resultado es salir del negocio. Con esto se termina el árbol de decisiones en la forma presentada en la figura 6, denominado árbol en dos etapas, puesto que hay dos puntos de decisión.
El tamaño del árbol crece rápidamente. Un árbol apenas con 10 nodos de decisión puede tener cientos de resultados finales. El análisis computarizado para resolver el árbol y seleccionar el mejor camino de decisión resulta muy pronto esencial.

Figura 1. Árbol de decisión de dos etapas que identifica alternativas de decisión y resultados posibles.
Para utilizar el árbol de decisiones a fin de evaluar y seleccionar alternativas. Es preciso estimar la siguiente información adicional para cada rama:
 Probabilidad estimada de que cada resultado pueda ocurrir. Estas probabilidades deben sumar 1.0 para cada conjunto de resultados (ramas) que resultan de una decisión.
Probabilidad estimada de que cada resultado pueda ocurrir. Estas probabilidades deben sumar 1.0 para cada conjunto de resultados (ramas) que resultan de una decisión.
 Información económica para cada alternativa de decisión y resultado posible, tal como, inversión inicial y flujos de efectivo anuales.
Información económica para cada alternativa de decisión y resultado posible, tal como, inversión inicial y flujos de efectivo anuales.
Las decisiones se toman a partir de la estimación de probabilidad y la estimación del valor económico para cada rama de resultados. De ordinario se utiliza el valor presente en los cálculos de valor esperado del tipo de la ecuación (1). El procedimiento general para resolver el árbol mediante análisis VP es:
1. Empiece en la parte superior derecha del árbol. Determinar el valor VP para cada rama de resultado considerando el valor del dinero en el tiempo.
2. Calcule el valor esperado para cada alternativa de decisión.
E (decisión) = L (estimación de resultado) P (resultado) (2)
Donde la sumatoria incluye todos los resultados posibles para cada alternativa de decisión.
3. En cada nodo de decisión, seleccione el mejor valor E (de decisión), el costo mínimo para una situación de costos solamente, o el reintegro máximo si se estiman los ingresos y los costos.
4. Continúe moviéndose a la izquierda del árbol hacia la decisión de las raíces con el fin de seleccionar la mejor alternativa.
5. Trace el mejor camino de decisiones de regreso a través del árbol.
El siguiente ejemplo ilustra este procedimiento.
4) Se requiere una decisión bien sea para mercadear o para vender un nuevo invento. Si el producto es mercadeado, la siguiente decisión es hacerlo a nivel internacional o nacional. Suponga que los detalles de las ramas de resultados producen el árbol de decisiones de la figura 7. Para cada resultado se indican las probabilidades y el VP de los costos y beneficios (reintegro en $ millones). Determine la mejor decisión en el nodo de decisiones DI.


Figura 2. Solución de un árbol de decisiones con valores presentes establecidos.
Solución
Utilice el procedimiento anterior para determinar que la alternativa de decisión DI, de vender el invento, debe maximizar el reintegro.
1. Este ejemplo se ofrece el valor presente del reintegro.
2. Calcule el reintegro VP esperado para alternativas de los nodos D2 y D3 utilizando la ecuación (2). En la figura 8, a la derecha del nodo de decisión D2, los valores esperados de 14 y 0.2 en óvalos se determinan como:
E (decisión internacional) = 12(0.5) + 16(0.5) = 14
E (decisión nacional) = 4(0.4) – 3(0.4) – 1(0.2) = 0.2
Los reintegros VP esperados de 4.2 y 2 para D3 se calculan en forma similar.
3. Seleccione el reintegro esperado más grande en cada nodo de decisión. Éstos son 14 (internacional) D2, y 4.2 (internacional) en D3.
4. Calcule el reintegro esperado para las dos ramas DI.
E (decisión de mercado) = 14(0.2) + 4.2(0.8) = 6.16
E (decisión de vender) = 9(1.0) = 9
El valor esperado para la decisión de vender es simple puesto que el único resultado tiene un reintegro de 9. La alternativa nodal DI de vender genera el reintegro esperado más grande de 9.
5. El camino de reintegro VP esperado más grande es seleccionar la rama de venta en DI para obtener $9, 000,000 garantizados.
5) La ciudad de Blarney tiene un corredor de 0.3 millas de autopistas de tráfico pesado para repavimentar. La firma Ajax Construction Company ofrece dos métodos para hacerlo. El primero es una superficie de concreto por un costo de $150,000 y un cargo de mantenimiento anual de $1000.
El segundo método es una cobertura de asfalto con un costo inicial de $100,000 y un cargo de servicio anual de $2000. Sin embargo, Ajax también exigiría que cada tercer año la autopista fuera retocada con un costo de $7500.
La ciudad utiliza una TMAR igual a la tasa de interés sobre bonos de ingresos, 6% en este caso. (a) Determine el número de años de equilibrio para los dos métodos. Si la ciudad espera que la interestatal remplace este tramo de autopista en 20 años, ¿cuál método debe seleccionarse? (b) Si el costo de retoque aumenta en $500 cada 0.1 milla cada 3 años, ¿es la decisión sensible a este costo?
Solución
(a) Prepare las ecuaciones VA Y determine el valor n de equilibrio.
VA del concreto = VA de asfalto
-150,000(A/P,6%,n) – 1000 = -100,000(A/P,6%,n) – 2000
-7500 [  P/F,6%,j) ] (A/P,6%,n)
P/F,6%,j) ] (A/P,6%,n)
Donde j = 3, 6, 9,…, n. Esta relación se rescribe como:
-50,000(A/P,6%,n)+1000+7500[  P/F,6%,j) ](A/P,6%,n)= O (3)
P/F,6%,j) ](A/P,6%,n)= O (3)
Un valor de n = 39.6 satisface la ecuación, de manera que se requiere una vida de 40 años aproximadamente para lograr un equilibrio al 6%. Si se tiene en cuenta que la carretera se requiere sólo durante 20 años, debe construirse la superficie de asfalto.
(b) El costo total de retoque aumentará en $1500 cada 3 años. La ecuación (3) es ahora:
50,000(A/P,6%,n)+1000+�[7500+1500 PIF,6%j)(A/P,6%,n)]==O
PIF,6%j)(A/P,6%,n)]==O
donde j = 3, 6, 9, . . ., n. El punto de equilibrio es aproximadamente 21 años, lo cual favorece aún la superficie del asfalto pero sólo en un margen de 1 año. La decisión es técnicamente insensible al incremento establecido en el costo estimado del retoque de $500 por 0.1 de milla.
6) Valores esperados para una propuesta. La firma Holdar-XS Construction Company piensa construir un complejo de apartamentos cerca al borde de una colina parcialmente nivelada. El soporte para la tierra a un lado del complejo debe asegurar que no ocurrirá daño o perjuicio a los edificios u ocupantes durante la estación lluviosa. La cantidad de lluvia experimentada en un momento de tiempo puede causar potencialmente cuantías variables de daño. En la tabla 5 se detalla la probabilidad de ciertas lluvias (en pulgadas) dentro de un periodo de unas pocas horas y el costo inicial para construir una pared de apoyo que asegure protección cuando se presente la cantidad correspondiente de lluvia. La construcción de la pared de apoyo será financiada por un préstamo a 30 años con reembolso al 9% de interés compuesto anual.
Los registros indican que ha ocurrido un promedio de $20,000 en daños durante las fuertes lluvias complejos similares. Sin tener en cuenta intangibles importantes de seguridad humana, requisitos de seguro e impuestos sobre la renta, determine cuánto se debe gastar en la pared de soporte. Suponga para construir la pared se establece la TMAR al costo del capital de deuda, es decir, 9%.
|
Tabla 5. Costo de lluvias de pared de apoyo
|
|
Lluvia, en pulgadas
|
Probabilidad de que ocurran mayores lluvias
|
Costo de la pared de apoyo, $
|
|
2.0
|
0.3
|
10.000
|
|
2.5
|
0.1
|
15.000
|
|
3.0
|
0.05
|
22.000
|
|
3.5
|
0.01
|
30.000
|
|
4.0
|
0.005
|
42.000
|
Solución
Utilice un análisis VA para encontrar el plan más económico. Inicialmente, determine la relación VA el pago del préstamo y el costo esperado del daño para cada nivel de lluvia. Se utiliza la cifra de $20000, ya que esta presenta la mejor experiencia disponible del costo de los daños.
V A = reembolso del préstamo anual + costo esperado de los daños anuales
V A = costo de la pared(A/P, 9%; 30) + (-20,000) (probabilidad de mayores lluvias)
Para ilustración, el VA a 3.0 pulgadas es:
VA = -22,000 (A/P, 9%,30) – 20,000(0.05) = $-3141
Los valores VA resultantes en la tabla 6 indican que la selección más económica es la pared de $30,000 para protección contra un aguacero de 3.5 pulgadas. La pared de $22,000 para una lluvia de 3.0 pulgadas está en un segundo lugar cercano.
|
Tabla 6. Valor anual para diferentes paredes de apoyo
|
|
Lluvia, en pulgadas
|
Pared de apoyo, costo, $
|
Costo anual de préstamo, $
|
Daño anual esperado, $
|
VA, $
|
|
2.0
|
-10.000
|
-973
|
-6.000
|
-6.973
|
|
2.5
|
-15.000
|
-1.460
|
-2.000
|
-3.460
|
|
3.0
|
-22.000
|
-2.141
|
-1.000
|
-3.141
|
|
3.5
|
-30.000
|
-2.920
|
-200
|
-3120
|
|
4.0
|
-42.000
|
-4.088
|
-100
|
-4.188
|
Comentario
Cuando la gente se encuentra potencialmente en peligro se incluye a menudo un gran factor de seguridad. Entonces, en la toma de decisiones no se utilizan sólo los resultados del análisis económico. Al construir para proteger en un grado mayor que el realmente requerido en promedio, las probabilidades de daño se reducen y los costos reales se aumentan.
7) Un muchacho desea establecer una venta de periódicos en la cafetería de la universidad y tiene que decidir cuantos deberá comprar. Estima vagamente la cantidad que podría vender en 15, 20, 25 ó 30 periódicos (para simplificar la situación, se acepta que cantidades intermedias no ocurran). Por lo tanto considera que tendrá que adquirir 15, 20, 25, ó 30 periódicos.
Con esta información se puede construir una tabla de resultados que indique el número de periódicos faltantes o sobrantes, así:
|
Ventas
|
15
|
20
|
25
|
30
|
|
Compras
|
|
|
|
|
|
|
15
|
|
0
|
-5
|
-10
|
-15
|
|
20
|
|
5
|
0
|
-5
|
-10
|
|
25
|
|
10
|
5
|
0
|
-5
|
|
30
|
|
15
|
10
|
5
|
0
|
Para convertir estos resultados en pérdidas o ganancias monetarias se deben utilizar las siguientes formulas:
Cuando Compras > Ventas
Resultado = PV x Ventas – PC x Compras + PR x (compras – ventas)
Cuando Compras < Ventas
Resultado = PV x Compras – PC x Compras
Donde:
PV: Precio de venta de cada periódico = 600 $
PC: Precio de compra de cada periódico = 500 $
PR: Precio de venta de los periódicos sobrantes como retal de papel = 2.50 $
Por lo tanto, la tabla de ganancias que se conoce como matriz de resultados será:
|
Ventas
|
|
Compras
|
15
|
20
|
25
|
30
|
|
15
|
1500
|
1500
|
1500
|
1500
|
|
20
|
-987.50
|
2000
|
2000
|
2000
|
|
25
|
-3475
|
-487.50
|
2500
|
2500
|
|
30
|
-5962.50
|
-2.975
|
12.5
|
3000
|
En este caso, sin llegar a la completa ignorancia, el decisor no tiene, ni siquiera en forma subjetiva un estimativo de la probabilidad de ocurrencia de los diferentes eventos.
Conclusiones
Con el desarrollo de este trabajo se obtuvieron las conclusiones siguientes:
1. Los proyectos económicos que comprendan riesgos e incertidumbre son considerados casos no determinísticos.
2. El concepto de incertidumbre implica que no se asignan distribuciones de probabilidad (definidas en términos de sus parámetros, tales como la media y la desviación estándar).
3. El riesgo implica que sí se le puede asignar algún tipo de distribución probabilística.
4. El término incertidumbre se utiliza para indicar una situación de desconocimiento del futuro y el hecho mismo de impredictibilidad de los hechos.
5. No se puede garantizar que una inversión de los frutos deseados y en consecuencia es posible que no ocurra el evento en teoría cierto.
Recomendaciones
En función del análisis y conclusiones que se obtuvieron con esta investigación se recomiendan las acciones siguientes:
1. Considerar el análisis de riesgo e incertidumbre de inversión de un proyecto.
2. Considerar la distribución probabilística para la evaluación económica de un proyecto.
3. Considerar el análisis de los índices de rentabilidad para la evaluación económica de un proyecto.
4. Considerar las estimaciones empíricas (relativo a la experiencia) a la hora de evaluar económicamente un proyecto.
5. Tomar en cuenta el factor riesgo a la hora de invertir en una determinada comunidad o país, en base a su seguridad política y social.
Bibliografía
- www.analitica.com/va/economia/opinion/9805646.asp
- www.cesca.es/farmacio/aula/xarxes_neuronals/fernandez/shtd.html
- www.infonegocio.com.pe/areas/marketing/especiales/20112000mc.shtml
- www.sigsa.com/ealmf/publicaciones/gestion.htm
- www.javeriana.edu.co/decisiones/Riesgo_incertidumbre_on_line/
Publicado en Monografías.com. Post original aquí.
Si te ha interesado este post, no olvides dejarnos tus comentarios. También apreciamos que los compartas con tus amigos y contactos en las redes sociales. Muchas gracias.
Me gusta:
Me gusta Cargando...
Share
 La teoría prospectiva o teoría de aversión a las pérdidas afirma que las percepciones de beneficio y pérdida de las personas son asimétricas. Es decir, las personas tienen más miedo a sufrir una pérdida de lo que son atraídos por el posible beneficio. Si las personas se les da la opción de dos perspectivas diferentes, van a escoger el que se piensa que tiene menos posibilidades de terminar en una pérdida, en lugar de la que ofrece la mayor cantidad de ganancias.
La teoría prospectiva o teoría de aversión a las pérdidas afirma que las percepciones de beneficio y pérdida de las personas son asimétricas. Es decir, las personas tienen más miedo a sufrir una pérdida de lo que son atraídos por el posible beneficio. Si las personas se les da la opción de dos perspectivas diferentes, van a escoger el que se piensa que tiene menos posibilidades de terminar en una pérdida, en lugar de la que ofrece la mayor cantidad de ganancias.




 Decisión ahora:
Decisión ahora: Selección de decisiones dentro de 2 años:
Selección de decisiones dentro de 2 años: Probabilidad estimada de que cada resultado pueda ocurrir. Estas probabilidades deben sumar 1.0 para cada conjunto de resultados (ramas) que resultan de una decisión.
Probabilidad estimada de que cada resultado pueda ocurrir. Estas probabilidades deben sumar 1.0 para cada conjunto de resultados (ramas) que resultan de una decisión.
 P/F,6%,j) ] (A/P,6%,n)
P/F,6%,j) ] (A/P,6%,n) PIF,6%j)(A/P,6%,n)]==O
PIF,6%j)(A/P,6%,n)]==O

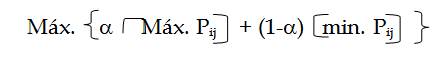
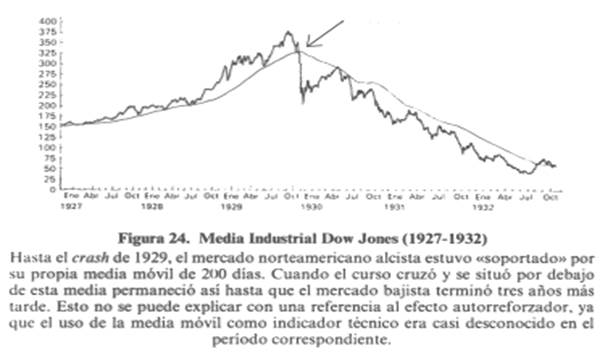
 En el ámbito de la psicología aplicada a la conducta económica destaca la figura de Daniel Kahneman, un autor americano-israelí cuya obra se ha centrado en los determinantes de la toma de decisiones en situaciones en que los beneficios y las pérdidas son inciertos.
En el ámbito de la psicología aplicada a la conducta económica destaca la figura de Daniel Kahneman, un autor americano-israelí cuya obra se ha centrado en los determinantes de la toma de decisiones en situaciones en que los beneficios y las pérdidas son inciertos.